城市再生水年利用量预测分析
导读:再生水指城市污水经适当再生工艺处理后,达到一定水质要求,满足某种使用功能要求,可以进行有益使用的水。随着社会经济的快速发展,城市污水排放量不断增加,加强以城市污水为水源的再生水利用开发有利于缓解水资源短缺、改善水生态环境。2021年6月印发的《“十四五”城镇污水处理及资源化利用发展规划》指出,“十四五”时期再生水发展的主要目标为全国地级及以上缺水城市再生水利用率达到25%以上,京津冀地区达到35%以上,黄河流域中下游地级及以上缺水城市力争达到30%。因此,为做好城市再生水利用规划,促进城市再生水事业发展,对城市再生水利用量进行预测具有很大的现实意义。
目前,国内外学者在大量研究的基础上提出了许多种再生水利用量的预测方法,主要有定额法、替代系数法、时间序列法、结构分析法、系统动力学法等。如汪妮等基于不同用水对象对再生水水质的不同要求,采用改进的灰色模型和定额法分别对回用于工业的再生水和市政杂用的再生水进行了需水量预测;王志坤等首先采用趋势分析法、定额分析法对城市再生水用水量进行了分析预测,并在此基础之上使用折减系数法计算了出城市再生水可利用量;余鹏明等运用相关性分析中的Spearman法分析了再生水利用量的影响因素,为进一步了解再生水利用发展状况以及利用量预测提供参考依据;唐莲等通过预测城市再生水可供水量和蓄水量,并依据供需平衡原理对城市再生水利用潜力进行了评估;李梅等建立了城市再生水利用系统动力学模型并对某城市的再生水利用预测进行了实践研究。
城市再生水年利用量过程呈现出很强的非线性特点,受到多种因素影响,且影响机制各不相同。常规方法如定额法、灰色模型预测法等较难在考虑这些影响因素的基础上做出精确预测。本文针对苏州市污水处理及再生水利用实际状况,基于其再生水年利用量各影响因素的历史数据较少、可靠性及完整性低等特点,采用灰色GM(1,1)模型对影响再生水年利用量的各因素进行预测,并以预测结果为输入因子,再建立BP神经网络预测模型预测苏州市城市再生水的年利用量。BP神经网络是人工神经网络中应用最为广泛的模型之一,具有学习速度快和适应能力强的优点,可对大多数非线性数据进行预测,且该模型能综合考虑再生水年利用量的各相关影响因素。故本文将灰色模型与BP神经网络模型相结合,以实现对城市再生水年利用量的有效预测,为城市再生水利用规划与合理配置提供决策依据。
一、研究区概况及再生水利用状况
1.1基本概况
苏州位于长江三角洲中部,地处30°47′N~32°02′N、119°55′E~121°20′E,东邻上海,南连浙江省嘉兴、湖州两市,西傍太湖,与无锡相接,北枕长江,总面积为8 657.32 km2,具体如图1所示。全市地势低平,境内河流纵横,湖泊众多。太湖水面绝大部分在苏州境内,河流、湖泊、滩涂面积占苏州市土地面积的36.6%,是著名的江南水乡,拥有各级河道2万多条,大小湖泊共300多个,著名的有太湖、阳澄湖、长江、京杭运河等。

图1 苏州市地理位置
1.2研究区再生水利用状况
苏州市自2018 年以来,以“高质量推进城乡生活污水治理三年行动计划”为基础,按照“苏州特别排放限值”要求,遵循江苏省住建厅提标改造技术指引,制定“一厂一策”提标方案,全力推进89 座城镇污水厂尾水提标改造。苏州市在全市开展城乡生活污水治理,项目化推进各项治理任务,确保污水厂提标改造的系统性和高效性;市政府及水主管部门强化组织领导,采取“成立专班,实体化运转办公;高位推动,强化部署推进;强化考核,加大推动力度”的管理方式,有力、有序、有效推进污水厂尾水提标改造任务。目前,全市城镇污水厂出水水质全面提标,达到苏州“准Ⅳ类”(除总氮外,其他指标均达到Ⅳ类标准)标准。根据相关数据统计,苏州市现状(2020年)年污水处理系统累计处理污水量为11.5亿m3。目前为止,完成提标改造的89座城镇污水厂出水水质均已达到《太湖地区城镇污水处理厂及重点工业行业主要水污染物排放限值》(DB 32/1072—2018)和“苏州特别排放限值”标准要求。各区市(县)污水处理厂分布以及再生水利用情况如表1所示。
表1 各区市(县)污水处理厂分布以及再生水利用

全市89座污水处理厂中:二类污水处理厂(20万~50万m3/d)有2座,均在工业园区;三类污水处理厂(10万~20万m3/d)有6座,吴中区1座、相城区1座、姑苏区2座、昆山市2座;四类污水处理厂20座(5万~10万m3/d);其余污水处理厂规模均在五类(1万~5万m3/d)及以下,污水处理能力较弱。
根据图2以及表1中数据:姑苏区再生水利用量及利用率分别为10 520.07万m3和88.30%,高于苏州其他区市,但是从利用途径分析,姑苏区再生水利用仅包括厂区自用及河道景观补水,其余利用方式均未涉及,且河道景观补水量约占再生水利用总量的98%,利用范围需要进一步扩大,充分发挥再生水潜力;再生水利用总量最少且利用率最低的为高新区,均被留作污水处理厂自用,考虑到区域内高新技术产业较多,这些产业对于生产用水的水质要求较高,目前的再生水出水水质暂时无法满足要求,因此,高新区内的污水处理厂需要进一步提高再生水处理水平;昆山市再生水利用量较多,达到了10 122.61万m3,其中约74%用于河道景观补水,3.4%留作厂区自用,约3.6%用于工业用水,约19%用于城市杂用水及其他用途,但是昆山市的再生水利用率仅为37.38%,这意味着还有大量处理后的污水没有得到有效利用,利用潜力巨大;其余区(市)中吴江区、工业园区再生水利用率相对较高,分为50.43%和47.00%,而相城区、张家港市、常熟市和太仓市利用率均在40.00%以下。

图2 各市(县)再生水利用量及利用率
经计算,苏州2020年城市再生水利用率为36.43%,主要用途为河道景观补水,占其再生水利用量的78.42%,利用形式较为单一。但随着再生水可利用量及其供水保证率逐步稳定,配套设施完善水平以及再生水管网覆盖率不断提高,苏州市再生水利用的规模和领域会继续扩大。
二、再生水利用量影响因素选择
2.1指标初步选取
本文所用的关于2008年—2020年苏州市再生水利用量系列,以及影响再生水利用量的主要因素等相关数据,主要来源于《城乡建设统计年鉴》以及《苏州市水资源公报》。
综合考虑经济、社会等多种影响再生水利用量的因素以及相关文献研究成果,初步选取影响再生水利用量的26个指标,如人均GDP、污水排放量、再生水生产能力、公共服务用水量、排水设施投资、污水集中处理率等
2.2SPSS相关性分析
上述根据分析选取的26个影响因子均会对城市再生水利用量产生一定影响,但影响程度轻重不一。故本文首先采用SPSS软件中的Spearman法对各个变量进行相关性分析以及显著性检验,并去除其中与再生水利用量相关性较低且不显著的变量,为下文进行BP神经网络预测选取合适的输入单元,提高预测精度。运用SPSS软件进行分析后,共选取了7个相关系数在0.65以上的指标,且相关性均为显著(P<0.05),具体数据如表2所示。
表2 影响因素分析结果
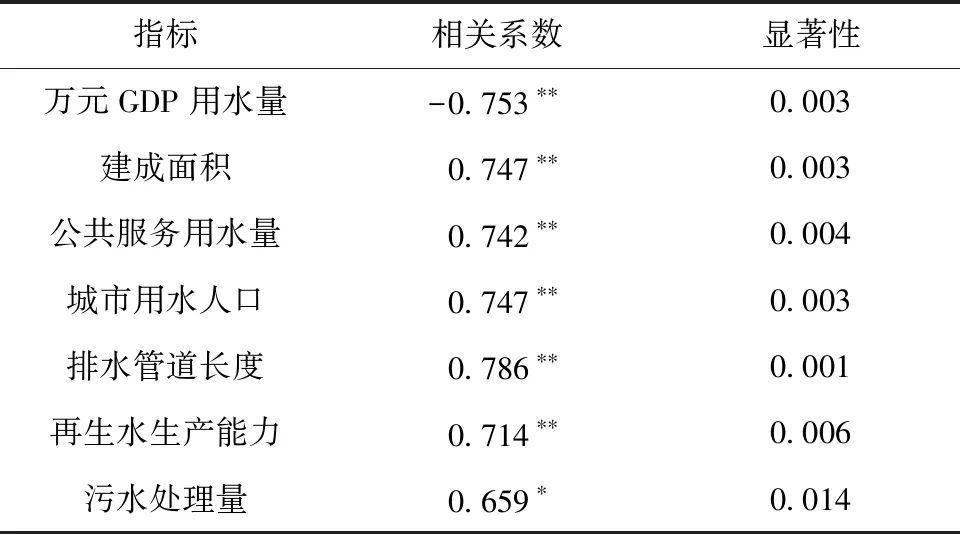
注:**表示在 0.01 级别(双尾),相关性显著;*表示在 0.05 级别(双尾),相关性显著。
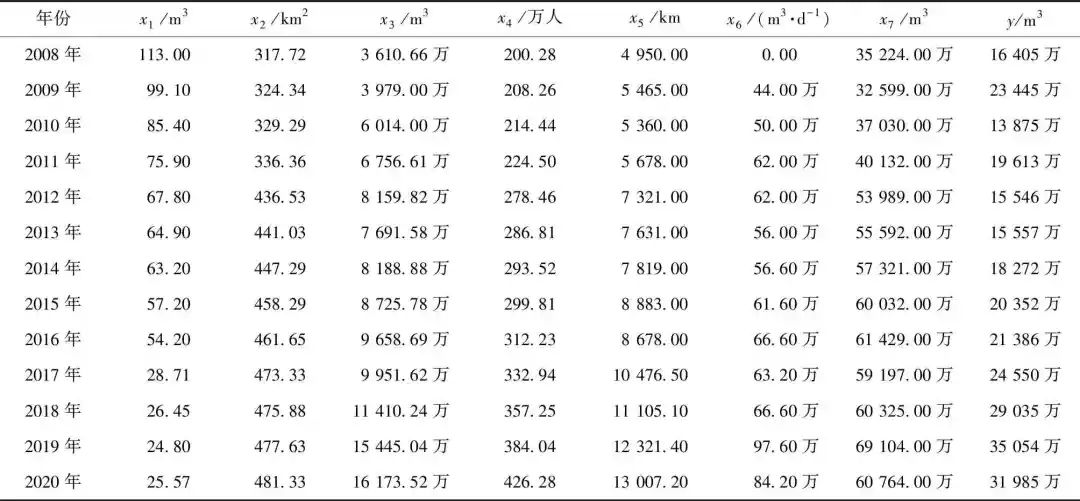
经相关性分析后选取的影响因子包括:x1为万元GDP用水量(m3),与再生水利用量呈显著负相关,万元GDP用水量的下降说明常规水资源以及再生水利用水平均有提升;x2为建成面积(km2),反映了市政公共设施及相应的污水收集措施的完善程度;x3为公共服务用水量(m3)、x4为城市用水人口(万人)、x7为污水处理量(m3),这些因素可直接影响再生水厂的进水水源;x5为排水管道长度(km),管道的完善有利于污水的收集和集中处理,增加再生水厂进水量;x6为再生水生产能力(m3/d),再生水生产能力的提升必然会直接促进城市再生水利用量及利用水平的进步。设y为再生水利用总量(m3),筛选后的主要影响因子及其具体数值如表3所示。
表3 苏州市再生水利用量及其主要影响因素数据
三、影响因素预测
3.1灰色预测模型GM(1,1)原理
相较于统计趋势预测法、回归分析法等预测方法,灰色GM(1,1)预测模型对于历史数据的样本容量要求不高,且允许样本存在灰色信息,不要求样本具有一定的分布规律,计算也较为简便。并结合苏州市再生水年利用量各影响因素的历史数据较少、完整性较低的实际情况,本文选择了灰色GM(1,1)预测模型。灰色GM(1,1)模型的基本原理是采用累加等方法生成基于原始数据序列的一次累加序列,并根据此序列建立预测模型,之后采取累减方法还原原始序列,输出预测结果。其建模过程如下。
设原始数据为x(0)=x(0)(1),x(0)(2),…,x(0)(n),其累加得到新的数据序列为x(1)=x(1)(1),x(1)(2),…,x(1)(n),其中
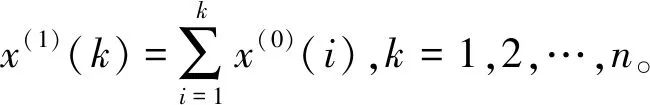
白化形式微分方程如式(1)。
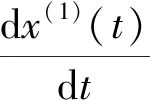
(1)
其中:a——发展系数;
u——灰色作用量;
t——时间序列。
记a、u构成的矩阵为灰参数
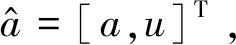
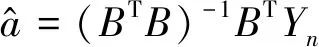
(2)
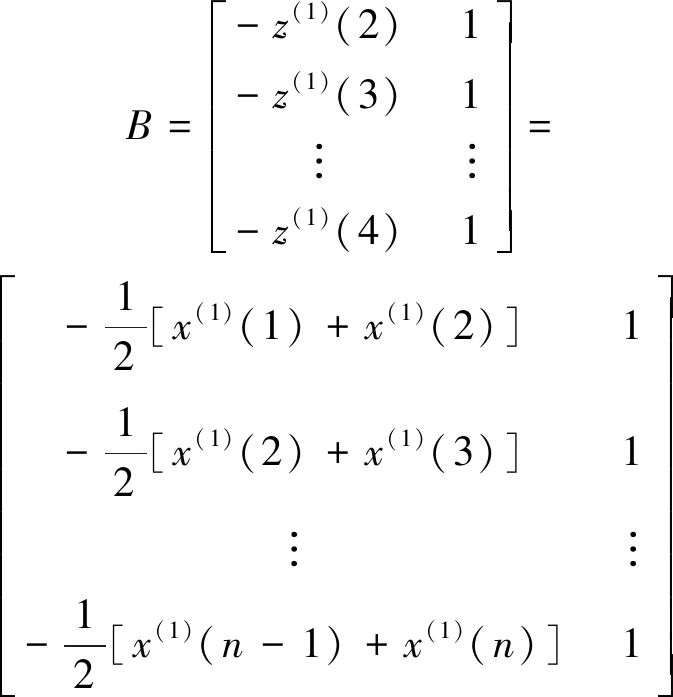
(3)
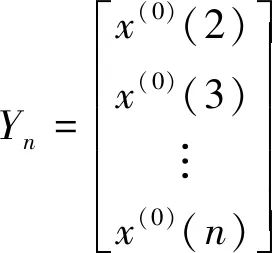
(4)
白化形式的微分方程的离散解如式(5)。
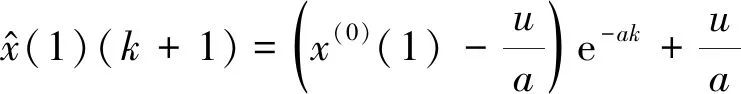
(5)
预测值计算如式(6)。
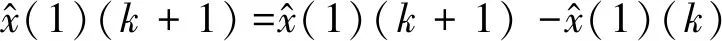
(6)
3.2基于灰色GM(1,1)模型的再生水利用量影响因素数据预测
以2008年—2018年的再生水影响因素数据作为原始序列,预测2019年及2020年各影响因素的值,结果如表4所示。
表4 灰色模型预测2019年及2020年各影响因素的值

3.3模型精度检验
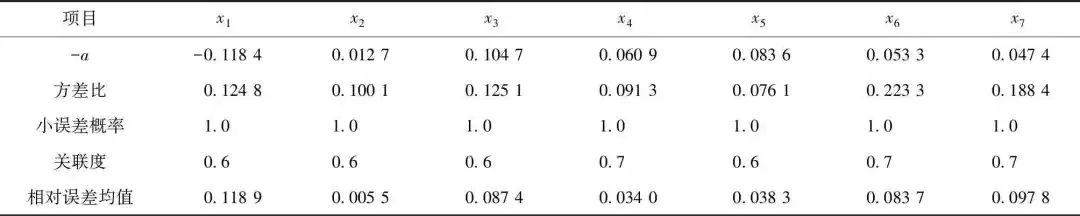
如表5所示,根据模型评价标准:因素x1~x7的-a系数均小于0.3,适合中长期预测;各因素的方差比均≤0.3,且小误差概率全为1,模型预测等级为好;关联度均在0.6~0.7,合格。模型基本满足各种检验,可用于再生水利用量各影响因素的中长期预测。
表5 模型精度检验结果
四、再生水年利用量预测
4.1BP神经网络原理
BP神经网络是一种由输入层、隐含层和输出层3层网状结构构成的多层前馈神经网络,本文采用含有一个隐含层的3层BP神经网络。数据信息通过输入层内的各节点进入网络,隐含层则可以对数据进行非线性转换后传输至输出层,理论上,含有一个隐含层的BP神经网络可表示任意输入和输出数据之间的映射关系。
BP算法的原理是将网络输出值与实际值的误差平方和作为网络的误差,输出误差由输出层至输入层逐层向前传播,同时误差将由各层所有单元分摊,各层之间的连接权重也会随之调整,权值调整完成之后,信号再次正向传播得到模拟输出值。通过这一循环过程,整个网络结构不断适应学习,使网络输出逼近期望值,最终误差达到设置的网络参数要求,循环停止。
4.2建立模型
本次研究共有13组数据,分别为2008年—2020年苏州市再生水利用量及其主要影响因子。其中,x1~x7这7个影响再生水利用量的因素为预测模型的输入值,再生水利用量为预测模型的输出值。将2008年—2018年的数据作为模型训练样本,2019年和2020年的数据则作为测试样本,同时为检验灰色GM(1,1)模型预测各因素对再生水预测精度的影响,将使用灰色模型预测所得的2019年及2020年的各影响因素的值同样作为测试样本,并与原始序列样本预测所得进行比较。由于影响再生水年利用量相关因素之间数据的量纲不同,数据范围相互差距较大,需要对其进行归一化,如式(7)。
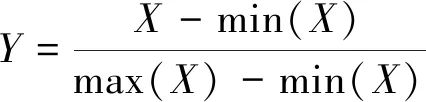
(7)
其中:Y——归一化后的输出数据;
X——原始输入数据;
min(X) ——X的最小值;
max(X) ——X的最大值。
4.2.1 BP模型各参数确定
本文采用仅含有一个隐含层的3层BP神经网络,输入层为7个影响再生水年利用量的变量,故输入层节点个数为7个,输出层节点1个。经过多次模型运行试验,并对比分析结果之后,确定隐含层节点个数为10个,网络参数设置如下:训练次数为50 000、学习速率和期望误差分别为0.06、0.000 01,此时模型运算结果最佳。隐含层节点的个数靠式(8)确定。激活函数选择单极性Sigmoid型函数。
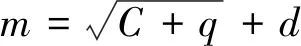
(8)
其中:m——隐含层节点个数;
C——输入层节点个数;
q——输出层节点个数;
d——0~10的整数。
4.2.2 网络训练结果
网络训练输出2008年—2018年再生水利用量预测值与实际值拟合情况如图3所示。由图3可知,BP神经网络模型输出的再生水利用量预测值较为准确,预测值与实际值平均相对误差仅为0.038%,其中最大相对误差为4.060%,最小相对误差仅为0.008%,与实际再生水年利用量极为接近,这充分说明BP神经网络模型具有较高的预测精度。
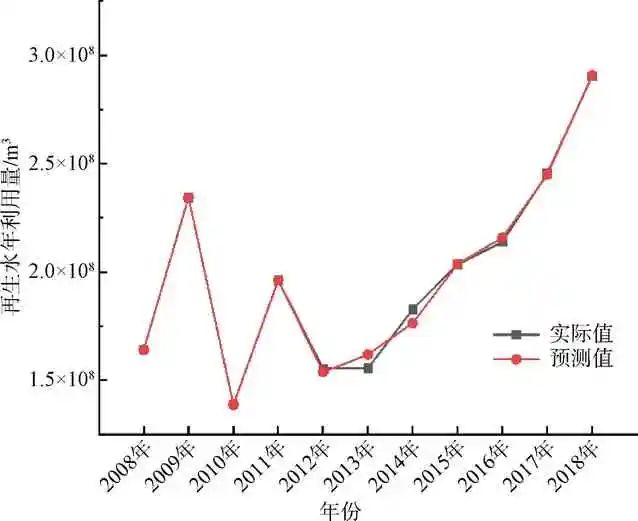
图3 BP神经网络模型训练结果
选取标准化平均偏差、标准化平均误差、平均绝对百分比误差、均方根误差作为预测模型的特征指标,结果见表6。可以看出,标准化平均偏差、标准化平均误差及平均绝对百分比误差的值均较小,均方根误差为280.78。根据以上分析,BP神经网络模型训练结果良好。BP神经网络经过足够的训练之后,必定可以满足设定的网络误差,且根据训练结果,网络学习的效率高,收敛较快,误差率小,模型预测结果符合设计要求。
表6 模型特征指标

4.3预测结果及分析
可利用本模型对2019年—2020年苏州市再生水利用量进行预测检验,分别将2019年和2020年原始数据以及灰色模型预测数据作为测试集,进行归一化输入BP神经网络模型后可得到预测结果如表7所示。由表中结果分析,模型分别根据原始数据及灰色GM(1,1)预测数据输出的苏州市再生水利用量预测结果与实际利用量拟合度较高,预测误差的绝对值均小于1%,精度等级较高。故以灰色GM(1,1)模型预测各再生水利用量影响因素的值作为BP神经网络的输入单元来预测再生水利用量的方法是可行的。以此方法得到的2021年、2022年及2025年的苏州市再生水利用量预测值如表7所示。
表7 预测结果及误差

五、结论
本文利用灰色GM(1,1)模型预测再生水利用量各影响因素的值,并以此作为BP神经网络模型的输入单元对苏州市城市再生水利用量进行预测,得到结论如下。
(1)根据相关性分析结果,苏州市再生水利用量的主要影响因素有万元GDP用水量、建成面积、公共服务用水量、城市用水人口、排水管道长度、再生水生产能力以及污水处理量7个指标,其中除万元GDP用水量与再生水利用量呈显著负相关外,其余指标均为显著正相关。由此可知,苏州市在提高用水及水处理效率、完善城市供水排水设施等方面还有较大的发展空间,城市再生水利用发展潜力巨大。
(2)灰色GM(1,1)预测模型不需要大量样本,且样本不需要规律分布,计算也较为简便。故本文采用该模型对再生水利用量各影响因素进行预测,预测结果满足方差比、小误差概率以及关联度等各种检验,预测精度较好,可用于再生水利用量各影响因素的中长期预测。
(3)考虑到城市再生水年利用量过程及其影响因素基础数据序列较少且具有随机性、非线性等特点,本文组合采用了灰色GM(1,1)模型和BP神经网络模型,不仅对各因素未来几年的数据进行了预测,同时也综合考虑了其对城市再生水年利用量的影响,提升了模型预测结果准确度和可靠性。分析表明,以原始序列数据及灰色GM(1,1)模型预测数据分别作为网络检验输入单元,预测苏州市2019年及2020年城市再生水利用量,输出结果精度均较高,验证了该方法的可行性及有效性,并对苏州市2021年、2022年及2025年的城市再生水利用量进行了预测,分别为35 478.53万、39 804.10万、46 404.85万m3。该方法适用于再生水利用发展较晚、利用量及其影响因素历史数据少的城市,可为城市再生水利用量的评估以及完善再生水利用规划提供参考依据。
推荐引用
本文来源于《净水技术》2023年第4期“污水处理与回用”,原标题为《城市再生水年利用量预测分析》,作者为侯金甫,方红远*,李艳明,程倩倩(扬州大学水利科学与工程学院,江苏扬州 225009),引用格式如下:
侯金甫,方红远,李艳明,等.城市再生水年利用量预测分析[J].净水技术,2023,42(4):95-102.
HOU J F,FANG H Y,LI Y M,et al.Prediction analysis of annual utilization of urban reclaimed water[J].Water Purification Technology,2023,42(4):95-102.