基于未来水量预测的污水处理厂旱天平稳运行策略研究
01、研究现状
在排水量的预测方面,常用模型可以归为:①解释性预测,即基于各类相关参数指标的回归模型,例如根据人口,气温,降水等参数建立模型;②时间序列分析,只依赖于被观测量的历史数据,通过分析找出规律再对下一时刻行预测。时间序列分析方法主流采用滑动平均MA,自回归模型AR,灰色模型GM,神经网络等。滑动平均法是较为基础也比较通用的方法,但精度较低,单一使用难以取得良好预测效果,GM模型则是用于处理样本量较少数据的手段。此外,神经网络模型在近几年大幅兴起,其中长短时记忆LSTM神经网络是处理时间序列问题十分主流的方法,一维卷积也是可选的方案,但神经网略缺乏可解释性,对于样本量较少的问题十分容易过拟合导致模型难以外拓,模型可信度较差,而自回归模型AR是处理时间序列的一种常用手段,能够描述当前时刻数据与历史数据之间的线性依赖关系,但是要求数据平稳因此往往与MA方法一同使用,为了获得平稳的数据也有采用差分作预处理的ARIMA方法。基于上述几类基本方法,也有大量研究对混合模型进行了探索。本次项目的数据仅包括来水量和降雨,不足以涵盖排水量的主要影响参数,并且解释性模型难以处理水量波动,因此基于时间序列分析展开。
已有方法均在水量预测上取得一定的成效,但目前所有的时序分析都没有充分利用时间序列在不同尺度上的模式特征。而排水量在一天、一周、一年的这三个尺度上都将呈现不同的特征和规律性,因此将时间序列按照不同尺度进行时序分析是十分有必要的。另一方面当前的水量预测方案主要针对城市日用水总量,在排水预测上,尤其是瞬时排水量的预测尚且没有较为合适的方法,因此本文提出多层次的时序分析方法。将预测水量划分为未来24h总水量和未来24h排水模式曲线两部分进行估计,其中两部分均通过历史数据与实时数据采用滤波数据融合进行实时校正,以预测未来瞬时排水量,并基于预测水量对应提出一套末端排水量运行策略,以实现末端水厂的平稳运行。
02、研究对象
规划期,拟建、在建工程完工后,片区内主要设施如下:H-Ⅰ线,设计规模170万m³/d,峰值输送能力45m³/s,末端接入ZY1厂总配水井,通过总配水井分配后进入各厂,当来水量超过各厂处理能力时,污水进入ZT调蓄池;W-Ⅲ线,设计规模50万m³/d,峰值输送能力20.85m³/s,末端接入ZY2和ZY3厂,当W-Ⅲ来水超过ZY2、ZY3厂处理能力时,污水进入ZT调蓄池,见图1。
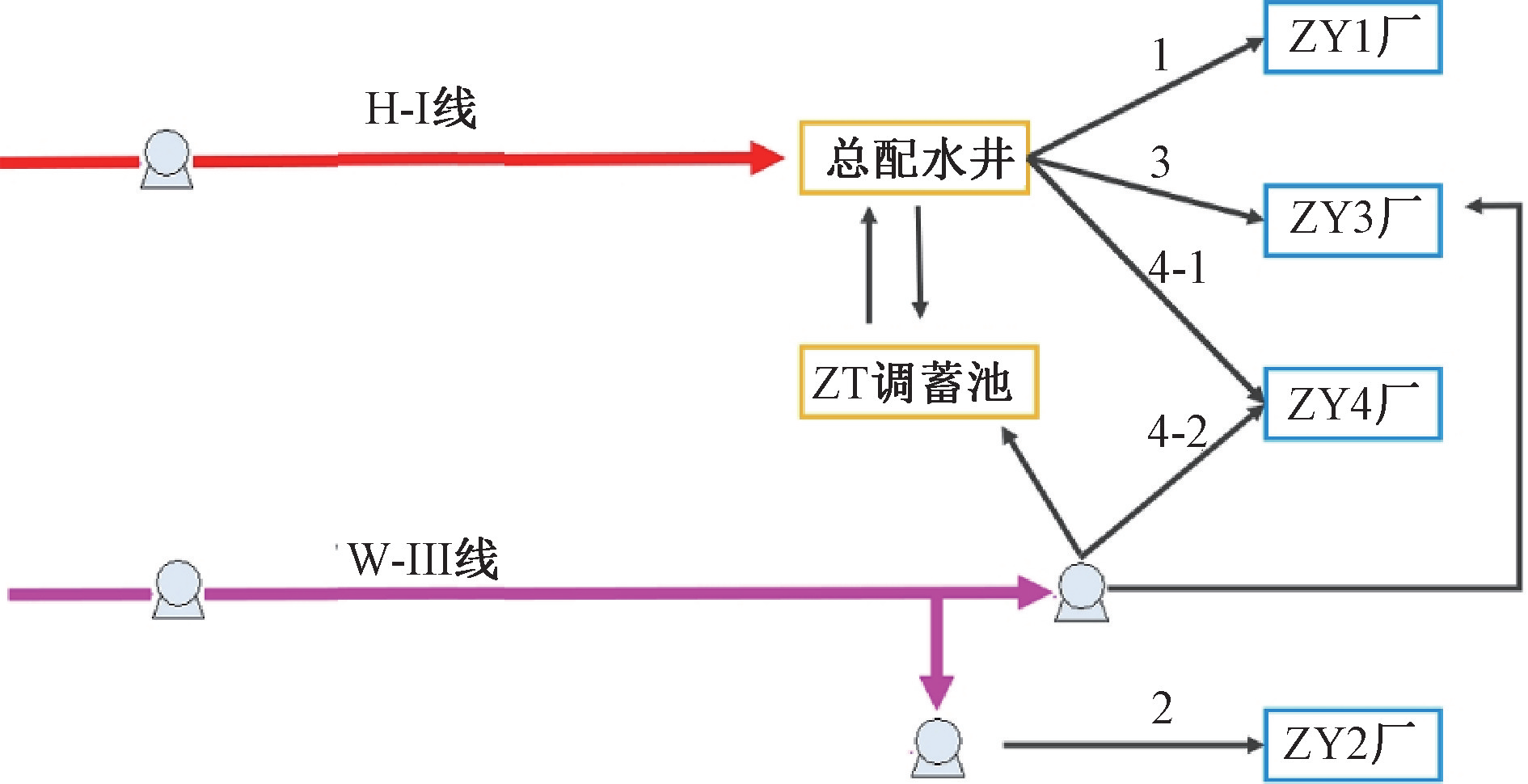
图1 片区末端水量分配
末端污水处理厂经多期建设,现状污水总处理规模220万m³/d,经多次功能改造、扩建,总体分三部分:ZY1厂处理规模110万m³/d,来水通过总配水井配水后进入ZY1厂;ZY2厂处理规模30万m³/d,来水通过W-Ⅲ线输送,由ZY2厂前提升泵房提升后进厂;ZY3厂处理规模80万m³/d,一部分来水通过总配水井配水后进入ZY3厂,另一部分水通过W-Ⅲ线末端提升泵站提升后进入ZY3厂;总配水井是厂内配水核心,H-I线末端提升泵站提升后污水进入总配水井进行配水,采用水电两用堰门方式应对水量变化实现配水。
在建ZY4污水处理厂,规模120万m³/d,来水通过总配水井配水;在建ZT调蓄池,总容积50万m³,当总配水井进水量超过各厂能力时,污水可进入调蓄池调蓄,当各厂处理能力有富余时,调蓄池启动放空泵将污水输送至总配水井,经调配后至各厂处理。
03、技术路线
根据实际情况,末端污水处理厂进水量视为由若干台水泵控制,忽略水泵实际工况,前后水位等对流量有影响的因素,视作单泵流量为定制进行计算,则出水量为以单泵流量为单位流量的量化值,最终的运行策略概化为在某一时刻决定开启的水泵数量,并维持尽可能长的时间。
经调研该污水处理厂旱天进厂水量仅238万~305万m³/d,且全天每小时水量波动大,全年各时段平均小时入流量6万~12万m³/h。因水量相对不稳定,各污水处理厂负荷大且波动大,可预测程度差,稳定运行难度较大。考虑利用历史数据建模,并根据实时数据进行矫正,以各污水处理厂运行稳定为目标,制定相关运行策略,具体流程见图2。
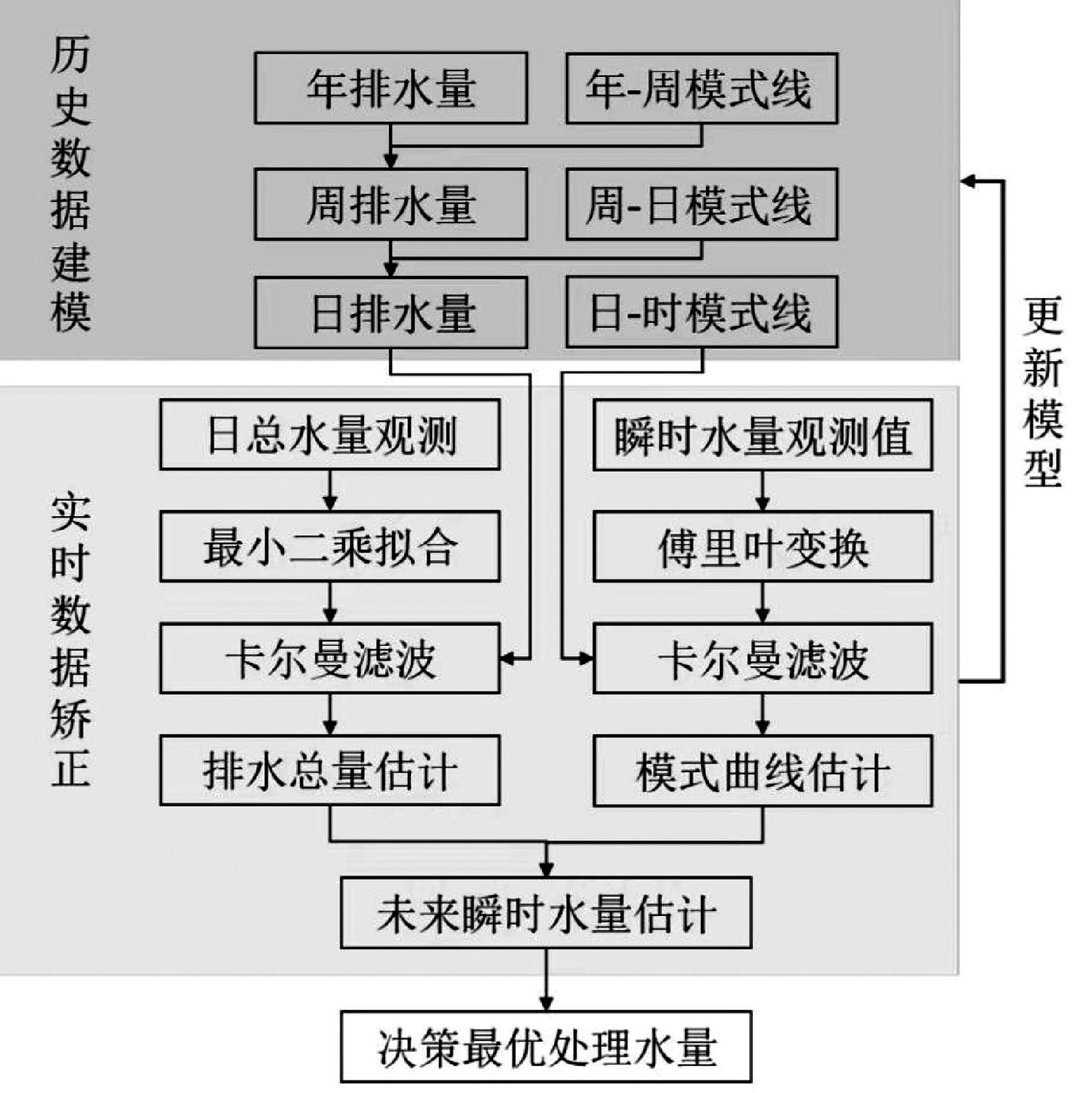
图2 研究框架
3.1 基于历史数据库构建未来水量预测模型
在不考虑雨天情况下,污水处理厂的进水量一般呈现日、周、月和年周期波动趋势。故根据已有的数据,排水末端的每5min流量和雨量计数据,为后续的污水处理厂运行水量控制提供预测和指导。
对于末端排水的水量预测按照其时间序列的特点,可以将其划分为不同的时间量化层次,当把所有的特殊工况去除后,天与天之间的时间模式具有一定的相似性,对于任何具备时间序列的特征可以用式(1)进行描述:
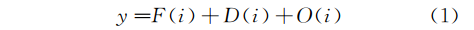
式中 i——基础的时间序列
F(i)——改时间序列中的规律项,在足够统计的时间长度下满足y-F(i)最小,称其为时间模式。
D(i)——时间序列中的波动项,或无规律项,又或由于现有数据不足表示的项,则使用统计下的概率分布来表示,同时又由于排水中分布的多样和复杂程度通常难以使用明确的分布公式所表示,并在实际的运行下,具体的分布形式难以对运行的指导意义比较有限,因此仅使用方差和期望两项对其进行表示,其中期望为0。
O(i)——观测误差,一般视作符合正态分布,虽然与D(i)通常不为同分布,但由于该项在排水中通常远小于D(i),故可忽略。
根据傅立叶变换,满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合,因此可以根据时间序列的实际意义结合实际运行工况,将函数拆分为分别以:1天、1周、1年,为周期的三个函数,见式(2):
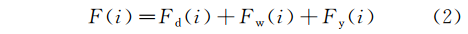
但在排水中,由于水量波动性的存在,通常可以通过累计一段时间的排水总量来消除一定的水量波动性。因此我们将时间模式分别以1 h、1 d、7 d为量化单位(时间步长)进行降采样并且对降采样部分做流量加和。则会得到不同时间尺度层次上的水量时间序列和评估指标见式(3)~式(7):
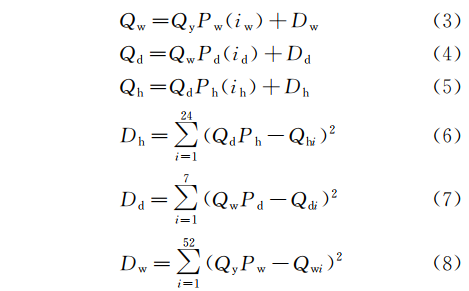
其中:Ph为以1h为步长,1天为一个观察周期的日时间模式;Qd为1天的排水总量;Qh为1小时的排水总量;Pd为以1 d为步长,1周为一个观察周期的周时间模式;Qw为1周的排水总量;Pw为以1周为步长,1年为一个观察周期的年时间模式;Qy为1年的排水总量;iw、id、ih分别为重采样后,对应时间模式下的时间序号;iw记为1年中的第i周;id记为1周中的第i天;ih为1天中的第i小时;Dh、Dd、Dw分别为重采样后,对应时间模式下的波动项。
假设总数据量为1年,以天时间模式为例,具体计算流程如下:首先按照1h的间隔重采样,并将时间序列写成[365×24]的矩阵形式记为Qh,同时按照1d的间隔重采样,并将时间序列写成[365×1]的矩阵形式记为Qd,为让Ph满足式(9)目标函数:
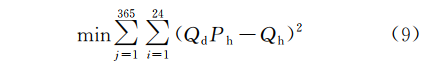
首先对对每日水量做归一化处理,即Qh[i,:]/Qd,然后对列求平均,见式(10):
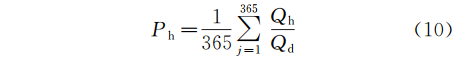
小时水量方差,见式(11):
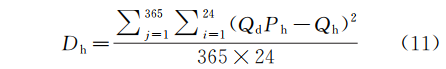
最终每小时用水量预测见式(12):
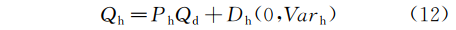
同理,根据以上原理生成周模式曲线和年模式曲线。
3.2 类卡尔曼滤波协同傅立叶变换的实时水量评估策略
未来水量的计算包括预测和修正两部分,还需考虑加入新数据后模型的更新。实时水量评估策略的主要目标有两个,分别为未来24 h排水总量和未来24h排水模式线。
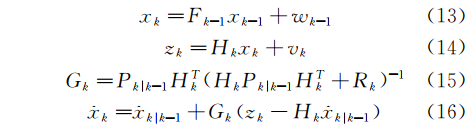
其中:xk为状态变量,表示为未知的系统状态参数;zk为观测变量,表示为系统的已知观测值;Hk为状态量x到观测量z的变化矩阵或构造矩阵;Pk为状态量估计的协方差矩阵;Rk为观测量的协方差矩阵。
由于在水量预测的前提下,是简单的一维模型,且观测量z即为状态量x因此上述矩阵式可以被简化为一维线性方程形式如式(17)和式(18):
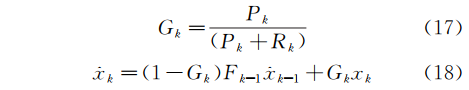
此处P即为预测模型的方差,R为观测误差的方差。
并且和传统滤波中略有区别的是:①本文使用的模型包含有方差项;②传统滤波通常为矫正当前时刻的观测状态,而在水量预测模型中,滤波的目的是辅助矫正后续一段时间内的水量预测,因此使用观测误差在这里就不再适用,需要根据目标替换。
3.3 未来24h排水总量估计
基于上文求得的预测模型可以计算出同期日用水估计,记作Qpre1,其标准差记作std1,见式(19)和式(20)。
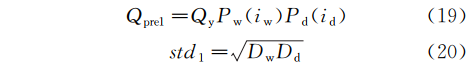
同理在日用水量层面也可以使用上述方法实时修正,但由于对于日用水量,短期数据基本不具备周期特征,并且根据实际经验可以视作基于一次线性函数外加随机分布,因此做一定程度简化。取前7日作为观测窗,将7日数据做最小二乘拟合求次日水量估计,记作Qpre2,并求出7日的标准差记作std2。
采用类卡尔曼滤波数据吸收的日水量估计记作Qpre3,其标准差记作std3,见式(21)和式(22):
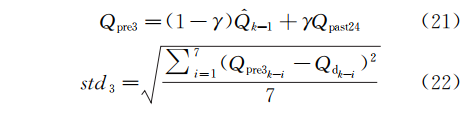
其中Qpast24为过去24小时实际排水总量;Q^k-1为上一时刻的未来24h排水总量估计;γ为数据吸收率,取0.1。
则下一时刻的的未来24h排水总量估计Q^d如式(23)所求:
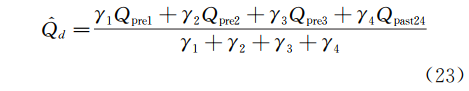
γ1、γ2、γ3、γ4为各项权重系数,可分别选用1/std1、1/std2、1/std3、1/std2。
3.4 未来24h排水模式线估计
首先求算当前时刻前24h的水量波动程度,具体做法如下:对这段时间的数据做离散傅立叶变换,得到排水量的频谱数据。根据蓄水池容积,裁减掉频谱的最高频段nmin参照式(24)~式(26):
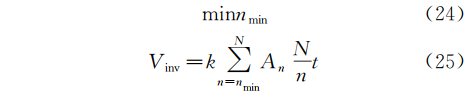
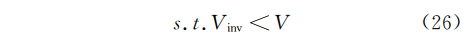
其中:An频率为n处波的振幅;N为时间窗口的量化单位时间数量;n为对应频率;t为量化单位时间的长度;k为控制的安全系数;V为蓄水池容积限值,Vinv为计算得到的虚拟蓄水池容积。
含义为各波段求积最大值之和小于蓄水池控制容积,本质上需要满足的条件为当污水处理厂按照平滑后的曲线当作进水量时蓄水池是否会超出容积上限。
经过傅立叶变换并压缩后变换回的平滑曲线记为Qf,则评估得到近24h的水量波动为,式(27)~式(30):
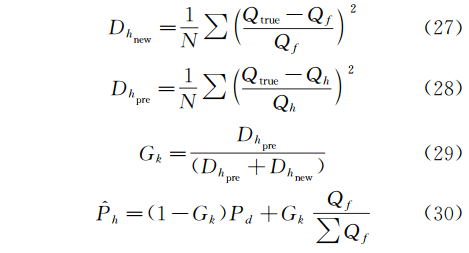
最终得到的未来24h瞬时排水量估计Q^h24为:
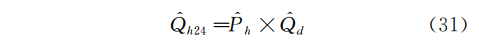
3.5 设计总处理水量
在本研究中,考虑到实际操作的可实施性,尽可能降低工人启闭阀门频次,因而将最终的设计处理水量设计为量化值×量化数的形式,或是理解为虚拟水泵单泵流量×开启数,则不同的n可以分别对应一个工况,则设计总处理水量Qtol计算见式(32):
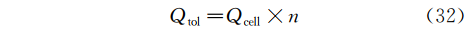
其中,Qcell为处理水量的量化值,即虚拟水泵流量,拟采用配水井出水泵的单泵流量2.93m³/s;n为当前决策的量化数,即虚拟水泵的开启数量。
决策时,假定保持当前总处理水量,根据前文方法求解的预测流量判断未来8h内蓄水池水量是否会超出蓄水池安全水量。当预测未来水水位大于Rsafe_max,虚拟水泵的开启数量n+1,反之若预测未来水位小于Rsafe_min,则n-1。蓄水池规定蓄水量按照式(33)和式(34)计算。
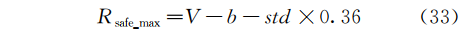
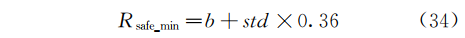
其中,Rsafe_max、Rsafe_min为蓄水池最大最小安全水量,万m³;V为蓄水池容积,万m³;b为人工设定的安全边界值,可取V的5%;std为历史水量预测准确程度的标准差Dh0.5。
04、实际运行结果
4.1 全厂进水量模拟结果
利用历史水量数据驯化模型,并根据来水情况评估预测准确性,并制定调度策略,对比实际运行数据评估策略稳定性。选取2020年中雨天较少的连续30天模拟实际运行结果。
其中图3展示了水量预测的实际效果,深绿色的瞬时水量预测尽可能地贴近了实际排水量的基础上消除了来水量的波动,能够在较长的时间尺度上预测未来来水量。
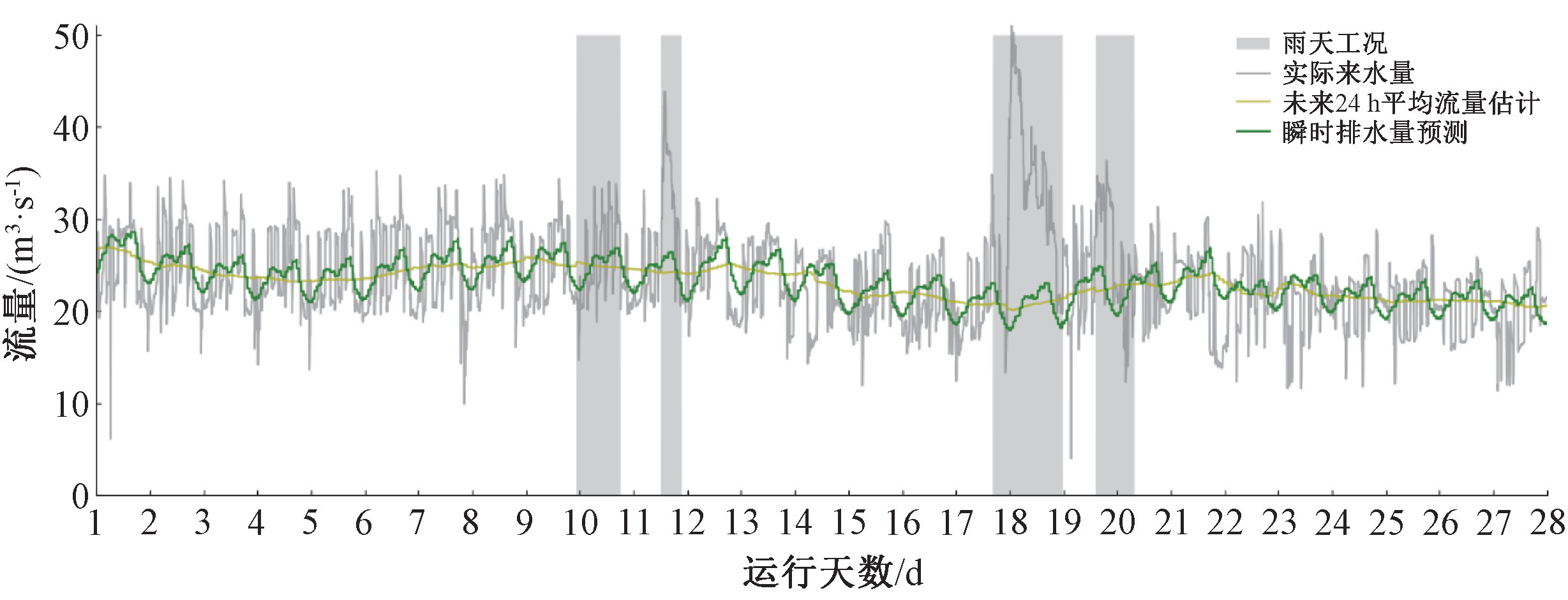
图3 水量预测实际运行效果
图4为在预测基础上决策计算得到设计处理水量,实现了十分理想的平稳性,避免了工况的频繁调整,并且保证了后续的水厂运行平稳。此外在保证蓄水池水量处在安全范围的基础上实现了蓄水池的充分利用,整体上实现了污水处理厂的平稳运行。
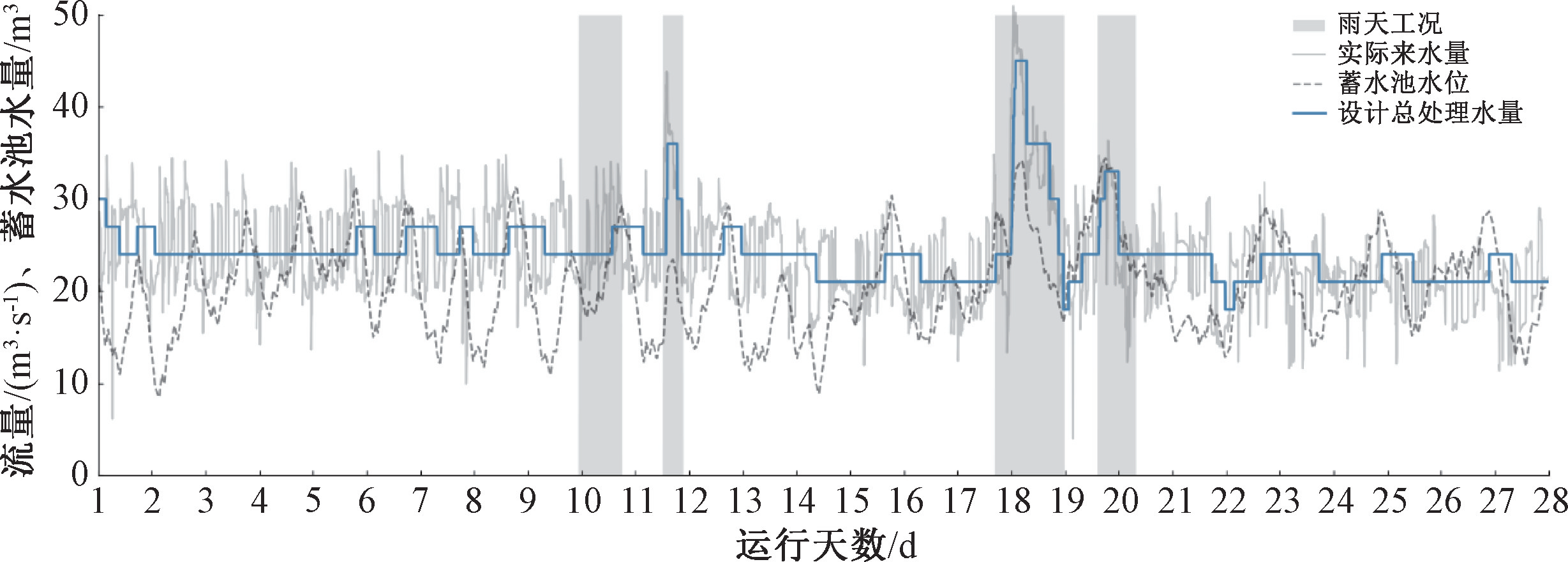
图4 设计总处理水量与蓄水池水位变化
4.2 各厂进水量模拟情况
水厂运行稳定性主要考虑处理水量的平稳,则以前后时刻的处理水量差异为评价指标,对于运行时长为t的水厂处理水量序列Q,其运行水量稳定性指标k值计算如式(35):
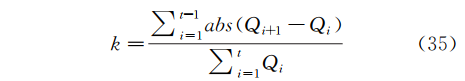
其中abs为绝对值计算符;Qi为水量时间序列Q在第i时刻的水量值。
由于ZY4厂处理水量构成走线较为复杂,实际处理量相较于设计量稳定性略有下降,但波动削减幅度依旧达到了85%,ZY2水厂因为作为第一个截流水量的水厂按照传统方法的稳定性相对较好,波动削减幅度为80%,而ZY1和ZY3的削减幅度则是能够达到94%。4座水厂均实现了稳定水量的目标,相较于传统方法,稳定性大幅度提高。
05、结论
(1)本文中提出的预测方法将未来水量划分为未来24h总水量和未来24h排水模式曲线两部分进行估计,其中两部分均通过历史数据与实时数据采用滤波数据融合,模式曲线得到合适的时间量化单位避免了水量的锯齿状波动,结合总水量,尽管在瞬时值上无法预测,但在更长的时间尺度上能够得到可靠的未来水量估计。
(2)基于以上水量预测,得到了一套有效的末端处理水量的计算方法并对应得到了一套末端水厂的配水方案以及调蓄池水泵的启闭策略。
(3)在该方法下的实际运行案例中,对比传统策略末端水厂处理量的波动值k大幅削减,表明该运行策略能够有效保证水厂的平稳运行,极大程度发挥了蓄水池的调蓄效用。
表1 优化方法与传统方法运行波动量每小时k值对比