排水系统监测数据异常识别与修复方法实践与探索——异常数据识别(一)
数据预处理
时间序列数据归一化
数据归一化处理是机器学习中的一项挖掘数据的基础工作,不同方法及评价指标往往具有不同的量纲和量纲单位,这样就会产生多样的数据分析结果,为了缩小数量之间的相对关系以及消除指标之间的量纲影响,需要进行数据归一化处理,以解决数据指标之间的可比性。数据经过归一化处理后,各指标处于同一数量级,适合进行综合对比评价。
常用的数据归一化方法有以下三种:
(1) 最值归一化方法(min-max normalization, MMN):
也称为线性归一化或离差归一化,是对原始数据的线性变换,使结果值映射到[0, 1]或某个自定的区间之间。转换函数如式(1):
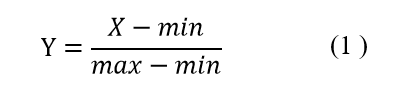
其中max为样本数据的最大值,min为样本数据的最小值,这种方法有个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义。
(2) 中值归一化方法(median normalization, MDN):
寻找原数据的中值,然后使用最大值最小值的差作为比例因子,然后将数据转化在某个区间内,一般是把零点作为区间中值,区间定为(-1, 1)。此方法多用于数据中没有错误样本,而只是单纯的将整个数据进行等比例的扩大或者缩小,转化函数为式( 2 ):
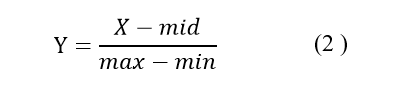
(3) 标准分数归一化方法(z-score normalization, ZSN):
这种方法给予原始数据的均值和标准差进行数据的标准化,经过处理的数据符合标准正态分布,即均值为0,标准差为1,转化函数为式(3):
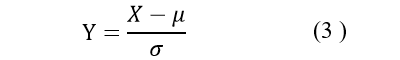
综上所述,本研究采用标准分数归一化方法,对原始城市排水管网系统数据进行归一化处理。
时间序列数据分割
时间序列线性划分是一种简单实用的时间序列划分方法。常用的三种线性分段算法有:滑动窗口技术(Sliding window, SW),自顶向下(top-down, TD),和自底向上(bottom-up, BU)。
这三种划分方法中,滑动窗口技术支持序列的在线划分,但是无法保留历史信息,划分效果欠佳;自顶向下和自底向上划分方式尽管划分效果较好,但需读取所有序列数据,无法实现在线分割。目前时间序列分类的方法大多都采用固定长度的时间窗进行划分,然后对截取的子序列进行聚类分析。
本研究使用固定长度和固定步长的滑动窗口(Sliding window,SW)技术对时间序列进行分割,生成模式序列数据。该方法简单可行,但也有其缺点。一方面,若滑动步长较小,则会造成大量的信息重复,有信息的冗余,若滑动步长较大,信息冗余减少,但可能会使信息提取不充分,错失关键信息点。另一方面,考虑到目标事件时间序列的拉伸性,该时间窗的宽度应大于平均异常事件的时长,然而若时间窗口宽度过大,则会在进行距离比较时引入较大的不确定性而不能很好地选择出相似时间。
因此基于实际异常事件出现的时长观察,本次研究拟选用时间窗口长度为1d,时间步长为5min,对原始数据归一化处理后的数据进行分割,以获取模式序列数据。
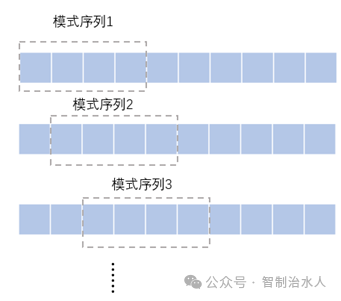
图1 滑动时间窗示意图
基于BF暴力算法的异常数据检测
BF暴力算法原理
BF算法,即暴力(Brute Force)算法,是普通的模式匹配算法。暴力算法的思想是,在通过长度为m的滑动窗口在长度为的时间序列上获取n-m+1个子序列后,得到大小为n-m+1的子序列集合,在这个集合中,将所有的子序列两两相比较,将最近邻最大的子序列输出为异常子序列。
暴力算法流程如表1所示:
表1 BF算法流程

将输入的时间序列按照指定的窗口长度进行两两的滑动比较,通过暴力解算的方式获取到若干个最邻近最大的异常子序列。其中:
Dist(tp,…,tp+m-1,tq,…,tq+m-1)
Dist函数主要获取子序列之间的两个特征距离,一个是欧式距离(Eudclidean Distance, ED)和动态时间扭曲距离(Dynamic Time Warping, DTW)。欧式距离是计算两个时间序列曲线距离的一种简单的方法,时间序列上对应时刻的绝对距离一一对应计算,然后获取两条曲线的欧式距离;而对于动态时间扭曲距离DTW,它表示的是两条曲线上,某一时刻的点可以同时对应另一条曲线上的多个点,相应的,反之另一条曲线上某一时刻也可以对应这条曲线上的多个点,也就意味着每个点尽可能地寻找离它距离最小的点,允许时间轴上存在拉伸和错位。DTW相较于ED更能够寻找到两条曲线之间的距离最小值,当时间序列上有拉伸或压缩时,DTW计算的距离更加的合理。
例如,有两个时间序列Cn={c1,…,cn},Qm={q1,…,cm},其欧式距离和DTW计算公式分别如式(2)-式(3):
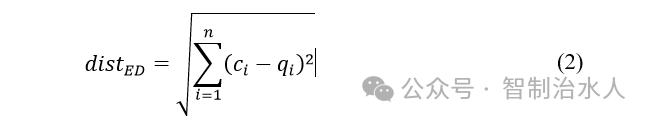
式中: distED——两个时间序列的欧式距离;
ci, qi——分别两个时间序列值;
其中要满足n=m;
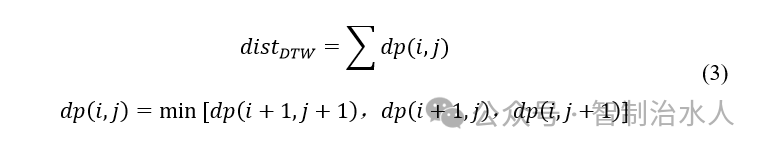
式中: distDTW——两个时间序列的动态时间扭曲距离;
dp(i,j) ——时间序列Cn中第i个位置与时间序列Qm中第j位置的欧式距离
基于BF暴力算法的泵站前池液位异常数据监测分析
对时间序列数据的暴力算法异常识别流程如图2所示,采用滑动窗口的方式对原时间序列进行子序列的分割,为了提高识别精度,避免错过单点的数据异常情况,窗口的滑动步长设为1,即以数据采集步长5min作为窗口的滑动步长。同时,窗口的长度的选取对于异常识别的准确度有着较高的影响。经过多次尝试,最终确定窗口长度为2h时,此时的缺陷识别能力最佳。
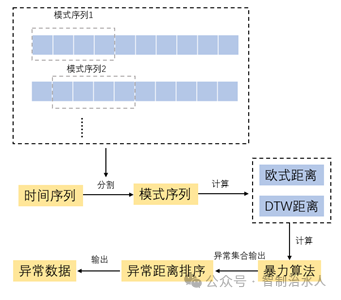
图2 基于BF暴力算法的异常识别流程图
由暴力算法识别的异常数据如图3所示:
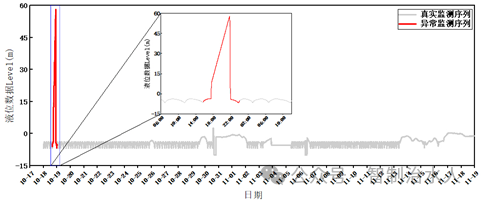
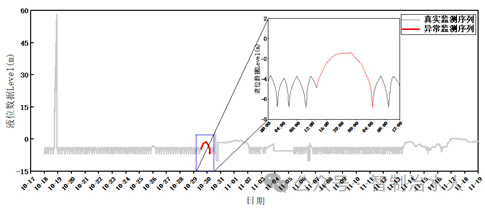
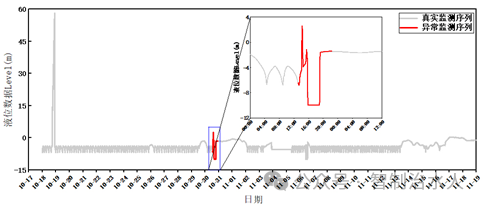
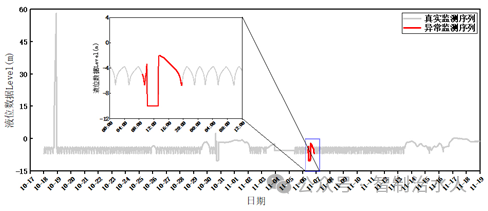
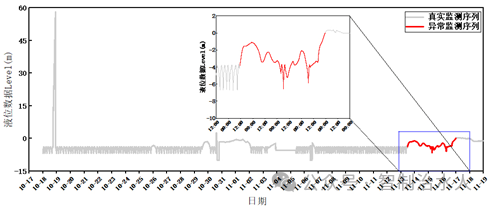
图3 基于BF算法的异常序列识别结果
由上图可知,基于BF算法对于液位数据中的异常有着较好的识别能力,如2020年10月18日 14:00:00 至 2020年10月19日 00:00:00 段,由于液位计发生短期故障,导致记录的数据持续上升,随后又恢复正常,BF暴力算法较好的侦测到此段异常,由于滑动窗口的长度为2h,且此处的异常属于突增异常,当窗口右边界进入“缺陷区域”时,较高的异常值快速导致该窗口的欧式距离和时间动态扭曲距离的快速增大,算法判断此窗口内含有“缺陷值”,并开始记录;随着窗口的滑动,当左边界滑出“缺陷区域”,此时的欧式距离和动态时间扭曲距离恢复为常规大小,算法停止记录。
但是该算法同样也存在着一定的缺陷性。如图中2020年11月3日12:00:00 至 2020年11月5日 12:00:00,在此期间,出现了较长时间的液位计掉线问题,此时的液位计无法记录正确数据,故导致较长时间段的0值数据,但是BF算法并没有正确的识别出次段的数据缺陷。分析主要原因在于,由于较长时间的0值数据(远大于窗口长度),导致窗口在此区域内滑动时,欧式距离以及动态时间扭曲距离均为0值,算法无法进行有效的判断。
作者简介
纪莎莎,上海城市建设设计研究总院(集团)有限公司研发中心主任,主要从事智慧排水相关设计研发工作,先后承担各类科研项目20余项,获得包括上海市科技进步奖、华夏建设科学技术奖在内的多个省部级科技奖项,个人曾获得上海市智慧工匠、上海市产业菁英、上海市城市之星、上海市水务海洋青年拔尖人才等多个称号。